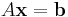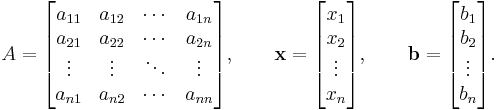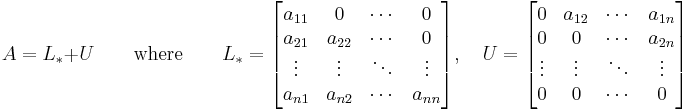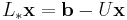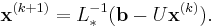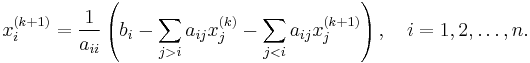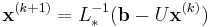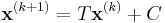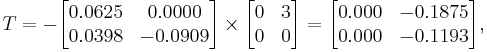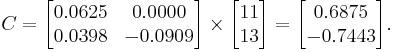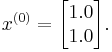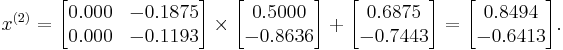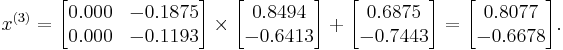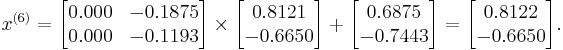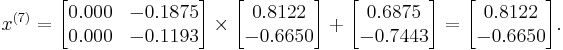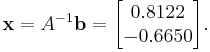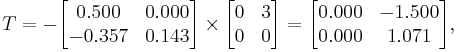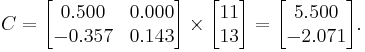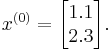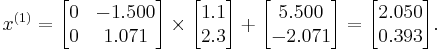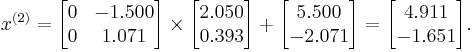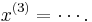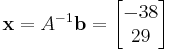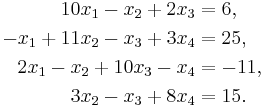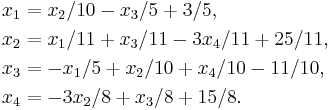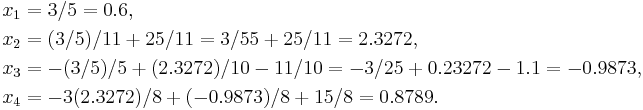Gauss–Seidel method
In numerical linear algebra, the Gauss–Seidel method, also known as the Liebmann method or the method of successive displacement, is an iterative method used to solve a linear system of equations. It is named after the German mathematicians Carl Friedrich Gauss and Philipp Ludwig von Seidel, and is similar to the Jacobi method. Though it can be applied to any matrix with non-zero elements on the diagonals, convergence is only guaranteed if the matrix is either diagonally dominant, or symmetric and positive definite.
Contents |
Description
Given a square system of n linear equations with unknown x:
where:
Then A can be decomposed into a lower triangular component L*, and a strictly upper triangular component U:
The system of linear equations may be rewritten as:
The Gauss–Seidel method is an iterative technique that solves the left hand side of this expression for x, using previous value for x on the right hand side. Analytically, this may be written as:
However, by taking advantage of the triangular form of L*, the elements of x(k+1) can be computed sequentially using forward substitution:
Note that the sum inside this computation of xi(k+1) requires each element in x(k) except xi(k) itself.
The procedure is generally continued until the changes made by an iteration are below some tolerance.
Discussion
The element-wise formula for the Gauss–Seidel method is extremely similar to that of the Jacobi method.
The computation of xi(k+1) uses only the elements of x(k+1) that have already been computed, and only the elements of x(k) that have not yet to be advanced to iteration k+1. This means that, unlike the Jacobi method, only one storage vector is required as elements can be overwritten as they are computed, which can be advantageous for very large problems.
However, unlike the Jacobi method, the computations for each element cannot be done in parallel. Furthermore, the values at each iteration are dependent on the order of the original equations.
Convergence
The convergence properties of the Gauss–Seidel method are dependent on the matrix A. Namely, the procedure is known to converge if either:
- A is symmetric positive-definite, or
- A is strictly or irreducibly diagonally dominant.
The Gauss–Seidel method sometimes converges even if these conditions are not satisfied.
Algorithm
Inputs: A , b
Output: 
Choose an initial guess 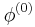 to the solution
to the solution
repeat until convergence
- for i from 1 until n do
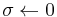
- for j from 1 until i-1 do
- end (j-loop)
- for j from i + 1 until n do
- end (j-loop)
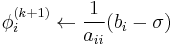
- end (i-loop)
- check if convergence is reached
end (repeat)
Gauss-Seidel is the same as SOR (successive over-relaxation) with 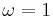 .
.
Examples
An example for the matrix version
A linear system shown as 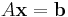 is given by:
is given by:
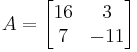 and
and 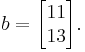
We want to use the equation
in the form
where:
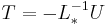 and
and 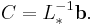
We must decompose 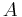 into the sum of a lower triangular component
into the sum of a lower triangular component 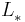 and a strict upper triangular component
and a strict upper triangular component 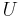 :
:
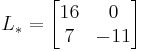 and
and 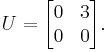
The inverse of 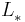 is:
is:
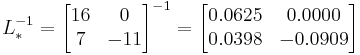 .
.
Now we can find:
Now we have 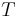 and
and 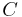 and we can use them to obtain the vectors
and we can use them to obtain the vectors 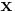 iteratively.
iteratively.
First of all, we have to choose 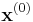 : we can only guess. The better the guess, the quicker the algorithm will perform.
: we can only guess. The better the guess, the quicker the algorithm will perform.
We suppose:
We can then calculate:
As expected, the algorithm converges to the exact solution:
In fact, the matrix A is diagonally dominant (but not positive definite).
Another example for the matrix version
Another linear system shown as 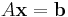 is given by:
is given by:
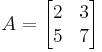 and
and 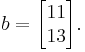
We want to use the equation
in the form
where:
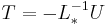 and
and 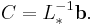
We must decompose 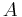 into the sum of a lower triangular component
into the sum of a lower triangular component 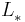 and a strict upper triangular component
and a strict upper triangular component 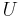 :
:
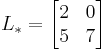 and
and 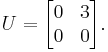
The inverse of 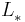 is:
is:
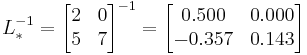 .
.
Now we can find:
Now we have 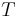 and
and 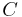 and we can use them to obtain the vectors
and we can use them to obtain the vectors 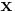 iteratively.
iteratively.
First of all, we have to choose 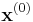 : we can only guess. The better the guess, the quicker will perform the algorithm.
: we can only guess. The better the guess, the quicker will perform the algorithm.
We suppose:
We can then calculate:
If we test for convergence we'll find that the algorithm diverges. In fact, the matrix A is neither diagonally dominant nor positive definite. Then, convergence to the exact solution
is not guaranteed and, in this case, will not occur.
An example for the equation version
Suppose given k equations where xn are vectors of these equations and starting point x0. From the first equation solve for x1 in terms of 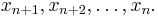 For the next equations substitute the previous values of xs.
For the next equations substitute the previous values of xs.
To make it clear let's consider an example.
Solving for 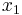 ,
, 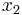 ,
, 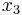 and
and 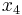 gives:
gives:
Suppose we choose (0, 0, 0, 0) as the initial approximation, then the first approximate solution is given by
Using the approximations obtained, the iterative procedure is repeated until the desired accuracy has been reached. The following are the approximated solutions after four iterations.
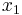 |
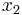 |
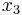 |
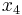 |
|---|---|---|---|
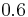 |
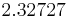 |
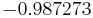 |
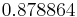 |
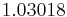 |
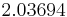 |
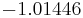 |
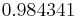 |
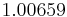 |
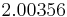 |
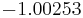 |
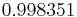 |
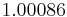 |
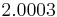 |
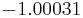 |
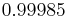 |
The exact solution of the system is (1, 2, −1, 1).
See also
- Jacobi method
- Successive over-relaxation
- Iterative method. Linear systems
- Gaussian belief propagation
References
- Black, Noel and Moore, Shirley, "Gauss-Seidel Method" from MathWorld.
This article incorporates text from the article Gauss-Seidel_method on CFD-Wiki that is under the GFDL license.
External links
- Gauss–Seidel from www.math-linux.com
- Module for Gauss–Seidel Iteration
- Gauss–Seidel From Holistic Numerical Methods Institute
- Gauss Siedel Iteration from www.geocities.com
- The Gauss-Seidel Method
- Bickson
- Matlab code
- C code example
|
||||||||||||||